アセンブリ言語 CASL2 論理演算のやり方と命令
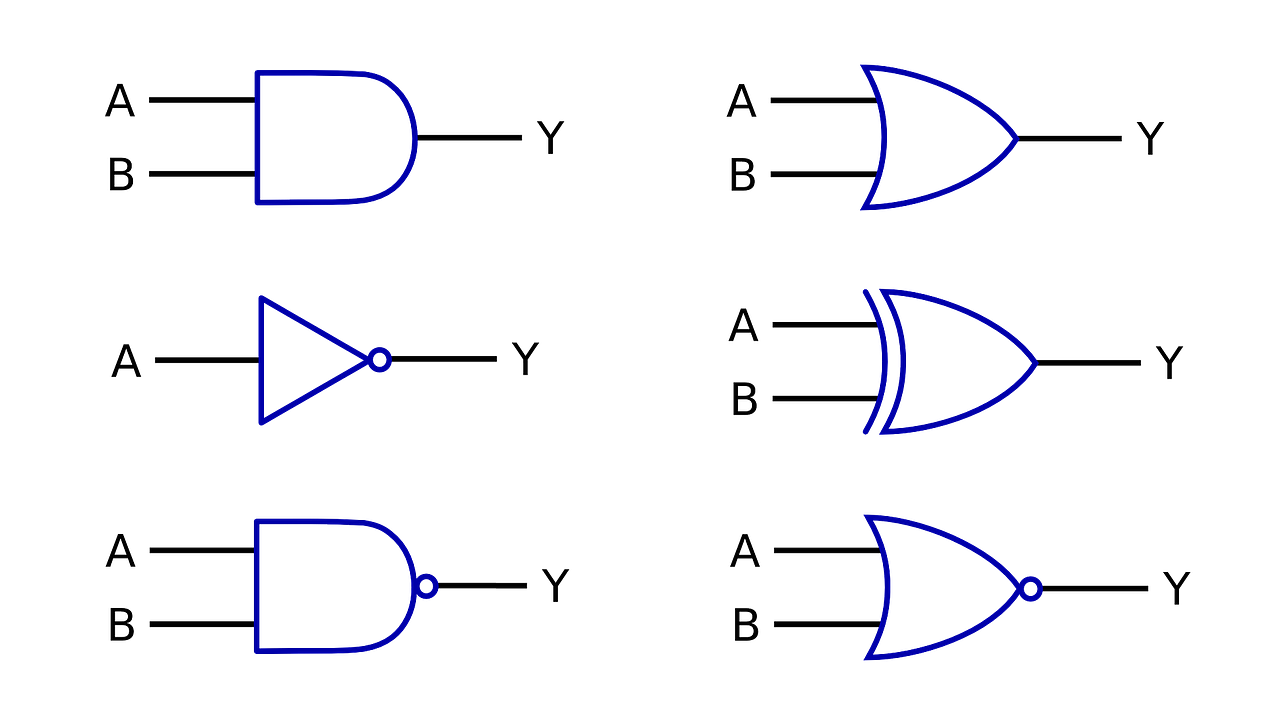
コンピューターは、足し算や引き算といった四則演算の他に、「論理演算」という計算を使うことがあります。
ただ、論理演算と聞くと何だか難しそうに聞こえますよね。でも、そこまで難しく考えなくても大丈夫です。
今回は、論理演算のやり方とCASL2で使える論理演算命令について見てみたいと思います。
論理積(AND)
論理積とは、1か0で表された数字A、Bが両方1であるときに答え(出力)が1になる計算です。
論理積は「AND演算」とも呼ばれます。「A AND B」「A ・ B」または単に「AB」という式で表します。
- 論理式: F = AB
かけ算の式と同じ記号(・)を使ったりしますが、普通のかけ算とは異なります。
論理積のイメージは、スイッチ2つをONにしないと点灯しない(スイッチ1つだけONにしただけでは点灯しない)電球と同じです。
【真理値表】| 入力 | 出力 | |
| A | B | F |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
上記の表は真理値表と呼ばれ、論理積における2つの入力に対する出力のすべてのパターンを表しています。
つまり、論理積の出力は真理値表に従って導き出せばいいということになります。
上記の真理値表に従い、入力AとBの両方が1のときに出力Fが1になります。
また、それ以外の入力のときは出力が0になります。
それでは具体的にどのような計算なのか見てみましょう。
例1: (0)2 AND (1)2 の論理演算
| 0 | |
| AND) | 1 |
| 0 |
入力AとBの両方が1で出力Fが1になります。
したがって、答え:(0)2になります。
論理積命令
| 名称 | オペコード | 第1オペランド | 第2オペランド | 第3オペランド |
| AND | AND | レジスタ | レジスタ or アドレス | --- |
| レジスタ | アドレス | レジスタ |
使用例1: AND GR0, A
汎用レジスタGR0の値とメモリA番地の値を論理積演算して、汎用レジスタGR0に転送(ロード)せよ。
使用例2: AND GR0, 1
汎用レジスタGR0の値とメモリ1番地の値を論理積演算して、汎用レジスタGR0に転送せよ。
使用例3: AND GR0, 1, GR1
汎用レジスタGR0の値とメモリ「汎用レジスタGR1の値 + 1」番地の値を論理積演算して、汎用レジスタGR0に転送せよ。
使用例4: AND GR0, GR1
汎用レジスタGR0の値と汎用レジスタGR1の値を論理積演算して、汎用レジスタGR0に転送せよ。
論理和(OR)
1か0で表せれた数字A、Bのどちらか一方が1であるときに答え(出力)が1になる計算です。
論理和は「OR演算」とも呼ばれ「A OR B」または「A + B」という式で表します。
- 論理式: F = A + B
論理和のイメージは、スイッチ2つある内のどちらかをONにすれば点灯する電球と同じです。
【真理値表】| 入力 | 出力 | |
| A | B | F |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
上記の真理値に従い、入力AかBのどちらかが1であれば出力Fが1になります。
それでは具体的にどのような計算なのか見てみましょう。
例2: (0)2 OR (1)2 の計算| 0 | |
| OR) | 1 |
| 1 |
入力AかBのどちらかが1なら出力Fは1になります。
また、A、B両方が0で、初めて出力0になります。
したがって、答え:(1)2になります。
論理和命令
| 名称 | オペコード | 第1オペランド | 第2オペランド | 第3オペランド |
| OR | OR | レジスタ | レジスタ or アドレス | --- |
| レジスタ | アドレス | レジスタ |
使用例1: OR GR0, A
汎用レジスタGR0の値とメモリA番地の値を論理和演算して、汎用レジスタGR0に転送(ロード)せよ。
使用例2: OR GR0, 1
汎用レジスタGR0の値とメモリ1番地の値を論理和演算して、汎用レジスタGR0に転送せよ。
使用例3: OR GR0, 1, GR1
汎用レジスタGR0の値とメモリ「汎用レジスタGR1の値 + 1」番地の値を論理和演算して、汎用レジスタGR0に転送せよ。
使用例4: OR GR0, GR1
汎用レジスタGR0の値と汎用レジスタGR1の値を論理和演算して、汎用レジスタGR0に転送せよ。
排他的論理和(XOR)
1か0で表せれた数字A、Bの値が異なる場合に、答え(出力)が1になる計算です。
排他的論理和は「XOR(またはEX-OR)演算」とも呼ばれ、「A XOR B」「A + B」または「AB + AB」という式で表します。
- 論理式1: F = A + B
- 論理式2: F = AB + AB
イメージとしてスイッチが2つある内、片方がONかOFFのとき点灯し、両方同じ場合に消灯する電球です。
ここで「+」という変な記号を使いますが、この論理演算は排他的論理和だ、と強調しているだけです。
排他的論理和はよく使う演算なので意味を持たせた演算子を用意したんだと思います。
特に難しい計算をしないといけないわけではないので、真理値表の通りに答え(出力)を求めればOKです。
【真理値表】| 入力 | 出力 | |
| A | B | F |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
上記真理値を見ると、入力AとBが異なる場合だけ、出力Fが1になっています。
A、Bの両方が同じ値のとき出力が無いため、「同じは嫌よ」と覚えてみてください。
例3: (1000)2 XOR (1001)2 の計算
| 1000 | |
| XOR) | 1001 |
| 0001 |
入力AとBが異なる場合、出力Fは1になります。
したがって、答え:(0001)2です。
排他的論理和命令
| 名称 | オペコード | 第1オペランド | 第2オペランド | 第3オペランド |
eXclusive OR | XOR | レジスタ | レジスタ or アドレス | --- |
| レジスタ | アドレス | レジスタ |
使用例1: XOR GR0, A
汎用レジスタGR0の値とメモリA番地の値を排他的論理和演算して、汎用レジスタGR0に転送(ロード)せよ。
使用例2: XOR GR0, 1
汎用レジスタGR0の値とメモリ1番地の値を排他的論理和演算して、汎用レジスタGR0に転送せよ。
使用例3: XOR GR0, 1, GR1
汎用レジスタGR0の値とメモリ「汎用レジスタGR1の値 + 1」番地の値を排他的論理和演算して、汎用レジスタGR0に転送せよ。
使用例4: XOR GR0, GR1
汎用レジスタGR0の値と汎用レジスタGR1の値を排他的論理和演算して、汎用レジスタGR0に転送せよ。
論理否定(NOT)
入力Aの反対のビット列が出力Fになります。
論理否定は「NOT演算」とも呼ばれ、「A」という式で表します。
- 論理式: F = A
【真理値表】
| 入力 | 出力 |
| A | F |
| 1 | 0 |
| 0 | 1 |
例4: (1000)2 の計算
- 1000 --ビット反転--> 0111
したがって、答え:(0111)2になります。
論理否定命令
実はCASL2には論理否定(NOT)演算用の命令はありません。
それではどうすればいいのか?
CASL2で論理否定の代わりに以下のような方法を使います。
例5: (1000)2 を論理否定したい場合| 1000 | |
| XOR) | 1111 |
| 0111 |
このように、同じ桁数のオール1のビット列と反転させたい数の排他的論理和演算を行うことで論理否定することができます。
さいごに
論理演算は、四則演算とは勝手が違うので初めは戸惑うかもしれません。
でも、真理値表はカンペみたいなもので、答え(出力)は初めから決まっています。
慣れない内は表の通り計算してしまえばOKです。
それでは次回にお会いしましょう。