【計算なし】補数を求める方法

補数の求め方って簡単なようで少し理解しにくいですよね。

実は、補数を求めるときにわざわざ計算しなくてもいいことをご存じですか？

今回は、2進数や10進数の補数を計算を使わずに求める方法を共有したいと思います。

補数は各進数に2種類ずつある

補数は各記数法に2種類ずつ存在します。

※ 記数法・・・2進数や10進数などの数の数え方をまとめた呼び方

例えば、10進数には9の補数と10の補数があり、2進数には1の補数と2の補数があります。加えて、16進数には15の補数と16の補数があります。

このように、補数という数は各n進数に2種類しか存在しないのです。

• 10進数・・・9の補数と10の補数
• 2進数 ・・・1の補数と2の補数
• 16進数・・・15の補数と16の補数

つまり、n進数の補数は「n-1の補数」と「nの補数」の2種類ある、という意味になります。

まずは、補数は各記数法に2種類ずつある、と覚えておけばOKです。

計算なしで補数を求める方法

それでは計算せずに10進数、2進数、および16進数の補数を求めてみます。

10進数の補数を求める

まず、10進数の補数を求める場合、9の補数から求めます。

そして9の補数を求めるには対応する数を反転させることで求めることができます。

いきなり「反転」といわれても意味不明ですよね。

反転とは以下の画像にあるような数の対応関係をいいます。

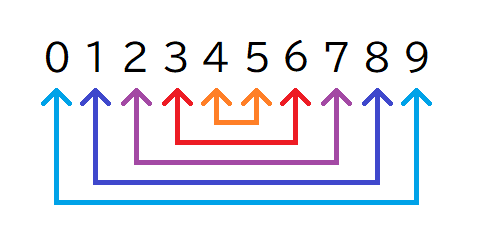
例えば、0の反転は9であり、2の反転は7であり、4の反転は5であるという意味です。

これが補数です。

つまり、10進数 7 の9の補数は 2 ということになります。また、10進数 1 の9の補数は 8 ということになります。

• 7 の9の補数 = 2
• 1 の9の補数 = 8

こう考えれば簡単ですよね。

そして、10の補数は9の補数に +1 した数ということです。

したがって、10進数 7 の10の補数は 3 になります。

また、10進数 1 の10の補数は 9 ということです。

• 7 の10の補数 = 7 の9の補数 + 1 = 3
• 1 の10の補数 = 1 の9の補数 + 1 = 9

10の補数を求めるときだけ1を加える計算を行っていますが、ほぼ計算せずに求めることができます。

2桁以上の9の補数と10の補数の求め方

2桁以上の9の補数は、対応する数の各桁を反転させれば求めることができます。

2桁以上の10進数の補数も9の補数から求めます。

例えば、10進数 15 の9の補数は 84 ということになります。

• 15 の9の補数 = 84

なぜなら「15」という数の10の位の「1」と1の位の「5」をそのまま反転させればOKだからです。

• 10進数 1 の9の補数 = 8
• 10進数 5 の9の補数 = 4

ちなみに、3桁以上になっても同ように各桁を反転させれば、簡単に補数を求めることができます。

もちろん、2桁以上の10の補数も9の補数に +1 するだけです。

したがって、10進数 15 の10の補数は 85 ということになります。

2進数の補数を求める

まず、2進数の補数を求める場合、1の補数から求めます。

1の補数を求めるには2進数の各桁を反転させることで求めることができます。

2進数における数の反転とは、0を1に、1を0にすることです。

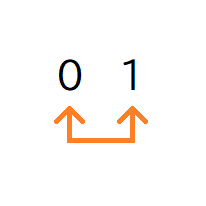
したがって、2進数 (1010)₂ の1の補数は (0101)₂ ということになります。

• 2進数 (1010)₂ の1の補数 = (0101)₂

2進数の各桁の1と0を入れ替える（反転）させればOKです。

2の補数の求めるには1の補数に +1 します。

つまり、2進数 (1010)₂ の2の補数は (0110)₂ ということになります。

• 2進数 (1010)₂ の2の補数 = 1の補数 + 1 = (0110)₂

16進数の補数を求める

16進数についても15の補数から求めます。

15の補数は16進数を反転させることで求めることができます。

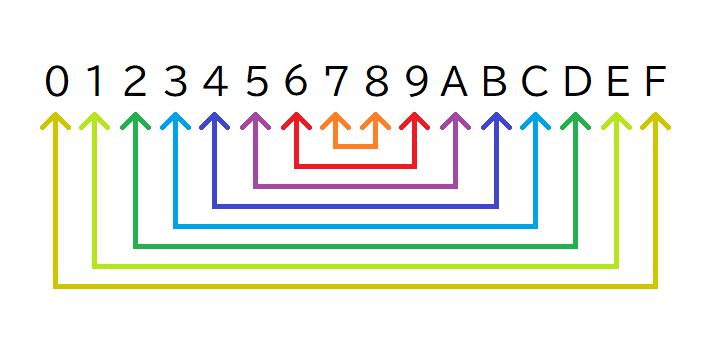
16進数の補数は、上の画像のように数がそれぞれ対応しています。

例えば16進数 (6A)₁₆ の補数を求める場合、各桁の (6)₁₆ と (A)₁₆ をそれぞれ反転させます。

そうすると (6)₁₆ の反転は (9)₁₆ であり、(A)₁₆ の反転は (5)₁₆ ということです。

• 16進数 (6)₁₆ の15の補数 = (9)₁₆
• 16進数 (A)₁₆ の15の補数 = (5)₁₆

よって、(6A)₁₆ の15の補数は (95)₁₆ になります。

そして16の補数は15の補数に +1 します。

よって、(95)₁₆ に1を加算すると (96)₁₆ になるので、(6A)₁₆の16の補数は (96)₁₆ ということです。

• 16進数 (6A)₁₆ の16の補数 = 15の補数 + 1 = (96)₁₆

補数とは合計すると1桁最大になる数のこと

nの補数とは、ある数と補数を合計するとnになる数のことです。

例えば、5の9の補数は4でしたよね？この5に補数である4を加算すると9になります。

• 5は4の9の補数・・・4 + 5 = 9

だから、4は5の「9の補数」であり、5は4の「9の補数」ということになるのです。

ということは、8の9の補数はいくつかというと... 9 - 8 = 1 ということが成立します。

そして「9」という数字は10進数1桁の最大の数ですよね。

これは、2進数の1・2の補数、16進数の15・16の補数も同じです。

さいごに

今回は計算しない補数の考え方について情報を共有しました。

まず、各記数法には2種類の補数が存在し、n進数の補数はn-1の補数とnの補数があること。

そして、例えば9の補数であれば、0～9の数をまず書き出して反転の関係になっている数を見れば、即求めることができます。

それでは次回にお会いしましょう。