アセンブリ言語 CASL2 で除算する方法

除算(わり算)を行うにはどうやったらいいと思いますか?
アセンブリ言語CASL2には除算を行う命令がありません。したがって、減算(引き算)を使って除算の機能を作る必要があります。
乗算(かけ算)は、例えば「2×4」なら2を4回足すことで計算できます。しかし、除算はどうやるのでしょうか。
今回は、CASL2による除算の方法について共有したいと思います。
ループ処理による除算
例1: 10 / 4 の計算
| 1 | MAIN | START | ||
| 2 | LD | GR1, A | ||
| 3 | LD | GR2, B | ||
| 4 | LAD | GR0, 0 | ;答え(商)格納用にGR0を初期化 | |
| 5 | ;------ エラー処理 ------ | |||
| 6 | CPA | GR1, =0 | ;わられる数と0を比較 | |
| 7 | JNZ | NX1 | ;わられる数が0でないならNX1に移動 | |
| 8 | LAD | GR1, 0 | ;わられる数を0に設定 | |
| 9 | RET | |||
| 10 | ||||
| 11 | NX1 | CPA | GR2, =0 | ;わる数と0を比較 |
| 12 | JNZ | NX2 | ;わられる数が0でないならNX1に移動 | |
| 13 | OUT | ERR, ERRLEN | ;エラー文出力 | |
| 14 | RET | |||
| 15 | ;------ エラー処理終わり ------ | |||
| 16 | NX2 | CALL | DIV | ;「DIV」サブルーチンの呼び出し |
| 17 | ST | GR0, ANS | ;答えをANS番地に格納 | |
| 18 | ST | GR1, MOD | ;わられる数(余り)をMOD番地に格納 | |
| 19 | RET | |||
| 20 | ||||
| 21 | DIV | CPA | GR1, GR2 | ;わられる数とわる数を比較 |
| 22 | JMI | FIN | ;わられる数がわる数より小さいならFINに移動 | |
| 23 | SUBA | GR1, GR2 | ;わられる数からわる数を引く | |
| 24 | ADDA | GR0, =1 | ;商に1を加算 | |
| 25 | JUMP | DIV | ;DIV番地に移動 | |
| 26 | FIN | RET | ||
| 27 | ||||
| 28 | A | DC | 10 | ;わられる数 |
| 29 | B | DC | 4 | ;わる数 |
| 30 | ANS | DS | 1 | ;答え |
| 31 | MOD | DS | 1 | ;余り |
| 32 | ERR | DC | 'ERROR' | ;エラー文字列 |
| 33 | ERRLEN | DC | 5 | ;エラー文字列の長さ |
| 34 | END | |||
※ シミュレータにそのままコピー&ペーストで使えます。
解説
ループ処理を用いた除算(割り算)は、わる数がわられる数より大きくなるまで、わられる数から1を引くことで実現しています。
除算の商(除算の答え)はわられる数が0になるまで1を引いた回数、余りはわられる数がわる数より小さくなった時点のわられる数ということになります。
- 商・・・わられる数が0になるまで1を引いた回数
- 余り・・・「わられる数 < わる数」になった時のわられる数
したがって、ループする毎にわられる数から割る数を減算することで除算になります。
また、コード上の赤字になっている5~13行はエラー処理です。
コードのエラー処理には、わる数やわられる数が0であった場合に、どのように処理すべきかが記してあります。
除算でのゼロの処理
除算は、わられる数が0のときは、商と余りの両方が0になります。
5~8行は、わられる数が0の場合の処理を行っています。
- 0 / 5 = 0...0 ・・・わられる数が0の場合
【わられる数が0の除算】
このように、わられる数が0の場合は必ず答えが0になります。
一方で割る数が0の場合はどうでしょうか。
除算は、わる数が0のときは「ゼロ除算」という、タブーに該当するため計算できません。
9~12行は、わる数が0の場合に除算を行うと、ゼロ除算という除算のタブーになるため、エラー文を出力し処理を終了します。
- 5 / 0 = 解なし...余りもなし ・・・わる数が0の場合
【わる数が0の除算】
除算では、どんな数であっても0でわることはできません。
じゃあ、なぜ0をわることができないのか?
例えば、「1 / 0.1」 の計算をすると答えは「10」になりますよね?
また、「1 / 0.01」のの計算ならどうなるかというと...答えは「100」です。
同ように「1 / 0.001」では「1000」になります。
つまり、わる数が0に近いほど商が巨大に膨れ上がってしまうのです。
このような性質から、ゼロ除算の商は無限大になってしまうのでタブーとなっています。
シフト演算による除算
例2: 10 / 4 の計算
| 1 | MAIN | START | ||
| 2 | LD | GR1, A | ||
| 3 | LD | GR2, B | ||
| 4 | LAD | GR0, 0 | ;答え(商)格納用にGR0を初期化 | |
| 5 | ;------ エラー処理 ------ | |||
| 6 | CPA | GR1, =0 | ;わられる数と0を比較 | |
| 7 | JNZ | NX1 | ;わられる数が0でないならにNX1移動 | |
| 8 | LAD | GR1, 0 | ;わられる数を0に設定 | |
| 9 | RET | |||
| 10 | ||||
| 11 | NX1 | CPA | GR2, =0 | ;わる数と0を比較 |
| 12 | JNZ | NX2 | ;わられる数が0でないならにNX2移動 | |
| 13 | OUT | ERR, ERRLEN | ;エラー文出力 | |
| 14 | RET | |||
| 15 | ;------ エラー処理終わり ------ | |||
| 16 | NX2 | CALL | DIV | ;「DIV」サブルーチンの呼び出し |
| 17 | ST | GR0, ANS | ;ANS番地に答えを格納 | |
| 18 | ST | GR1, MOD | ;MOD番地にわられる数(余り)を格納 | |
| 19 | RET | |||
| 20 | ||||
| 21 | DIV | LAD | GR3, #0001 | ;GR3に答えになる値を転送 |
| 22 | LD | GR4, GR2 | ;GR4にわる数の元の数を転送 | |
| 23 | LP1 | CPA | GR1, GR2 | ;わられる数とわる数を比較 |
| 24 | JMI | LP2 | ;わられる数がわる数より小さいならLP2に移動 | |
| 25 | SLL | GR2, 1 | ;わる数を2倍 | |
| 26 | SLL | GR3, 1 | ;答えになる値を2倍 | |
| 27 | JUMP | LP1 | ||
| 28 | LP2 | CPA | GR1, GR2 | ;わられる数とわる数を比較 |
| 29 | JMI | NX3 | ;わられる数がわる数より小さいならNX3に移動 | |
| 30 | ADDA | GR0, GR3 | ;答えに、答えになる値を加算 | |
| 31 | SUBA | GR1, GR2 | ;わられる数からわる数を減算 | |
| 32 | NX3 | SRL | GR2, 1 | ;わる数を1/2倍 |
| 33 | SRL | GR3, 1 | ;答えになる値を1/2倍 | |
| 34 | CPA | GR1, GR4 | ;わられる数とわる数の元の数を比較 | |
| 35 | JMI | FIN | ;わられる数がわる数の元の数より小さいならFINに移動 | |
| 36 | JUMP | LP2 | ||
| 37 | FIN | RET | ||
| 38 | ||||
| 39 | A | DC | 10 | ;わられる数 |
| 40 | B | DC | 4 | ;わる数 |
| 41 | ANS | DS | 1 | ;答え |
| 42 | MOD | DS | 1 | ;余り |
| 43 | ERR | DC | 'ERROR' | ;エラー文字列 |
| 44 | ERRLEN | DC | 5 | ;エラー文字列の長さ |
| 45 | END | |||
※ シミュレータにそのままコピー&ペーストで使えます。
解説
シフト演算による除算は、2進数の除算の筆算に基づいて組まれています。
このプログラムは、ループを用いた除算よりも行数は多いですが高速に動作するはずです。
例として2進数の除算を筆算で行う方法を以下に示します。
【10 / 4の計算】
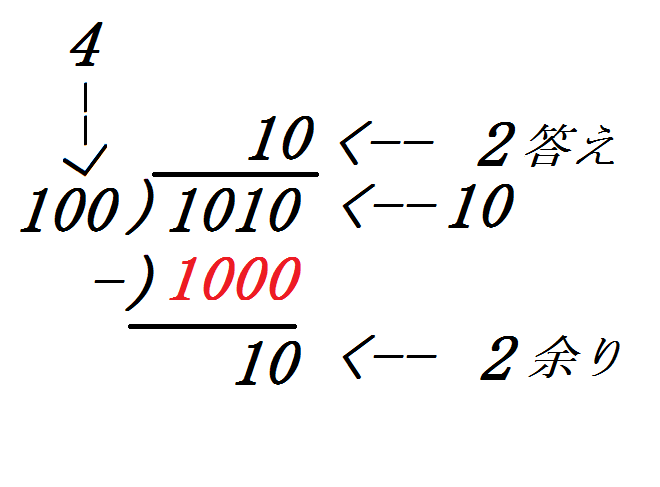
- まず、わられる数(10)とわる数(4)を2進数にして考える。
- 筆算の式にする。
- わる数(4)にどのくらいの数を掛ければ、わられる数(10)と同じか最も近い数になるかを考える。例えば...
わる数(4)に2を掛けると8になるので「答え」のところに2を書き込む。 - わられる数(10)から8を減算し、余り(2)が導き出される。
- 余り(2)は、わる数(4)より小さいので、商(2)と余り(2)が求められる。
「わられる数(余り) < わる数」 になったら計算を終了。
このような手順をCASL2でどうやって実現できるかを考えながらプログラムを組みます。
アルゴリズムの考え方は、プログラマー各人に委ねられているので、必ずしも上で紹介したプログラム通りに作らないといけないわけではありません。
「わたしだったらこうするかな」という感じで、他者が作ったプログラムにケチをつけるノリでプログラミングするのも手ですし、
他者のプログラムコードをまだ読めない場合は自分で一から考えてみるのが早いです。
再起処理による除算
例3: 10 / 4 の計算
| 1 | MAIN | START | ||
| 2 | LD | GR1, A | ||
| 3 | LD | GR2, B | ||
| 4 | LAD | GR0, 0 | ;答え(商)格納用にGR0を初期化 | |
| 5 | ;------ エラー処理 ------ | |||
| 6 | CPA | GR1, =0 | ;わられる数と0を比較 | |
| 7 | JNZ | NX1 | ;わられる数が0でないならにNX1移動 | |
| 8 | LAD | GR1, 0 | ;わられる数を0に設定 | |
| 9 | RET | |||
| 10 | ||||
| 11 | NX1 | CPA | GR2, =0 | ;わる数と0を比較 |
| 12 | JNZ | NX2 | ;わられる数が0でないならにNX2移動 | |
| 13 | OUT | ERR, ERRLEN | ;エラー文出力 | |
| 14 | RET | |||
| 15 | ;------ エラー処理終わり ------ | |||
| 16 | NX2 | CALL | DIV | ;DIVサブルーチンの行に移動 |
| 17 | ST | GR0, ANS | ;ANS番地に答えを格納 | |
| 18 | ST | GR1, MOD | ;わられる数(余り)をMOD番地に格納 | |
| 19 | RET | |||
| 20 | ||||
| 21 | DIV | CPA | GR1, GR2 | ;わられる数とわる数を比較 |
| 22 | JMI | FIN | ;わられる数がわる数よる小さいならFINに移動 | |
| 23 | SUBA | GR1, GR2 | ;わられる数からわる数を減算 | |
| 24 | ADDA | GR0, =1 | ;答えに1を加算 | |
| 25 | CALL | DIV | ;再起処理 | |
| 26 | FIN | RET | ||
| 27 | ||||
| 28 | A | DC | 10 | ;わられる数 |
| 29 | B | DC | 4 | ;わる数 |
| 30 | ANS | DS | 1 | ;答え |
| 31 | MOD | DS | 1 | ;余り |
| 32 | ERR | DC | 'ERROR' | ;エラー文 |
| 33 | ERRLEN | DC | 5 | ;エラー文字列 |
| 34 | END | |||
※ シミュレータにそのままコピー&ペーストで使えます。
解説
再起処理による除算は、ループ処理による除算のループが再起処理に置き換わったものです。
再起処理を用いた除算も、ループ処理を用いた除算と同じくわられる数がわる数より小さくなるまで、わられる数からわる数を減算します。
そのとき、わる数の値の分再起処理を行い、再起した回数をカウントしています。
そして、再起の回数が商で、わられる数がわる数より小さくなったときのわられる数が余りとなります。
- 商・・・カウントした再起の回数
- 余り・・・「わられる数 < わる数」になった時のわられる数
また、赤字になっている5~12行のコードはエラーの処理です。
商が正しいか確認する方法
蛇足ですが、商の確かめ算の方法を見てみたいと思います。
確かめ算は式を変形させることで、答えが正しいかを確かめる計算方法です。
除算は、商と余りが正しいかを以下の式によって確かめることができます。
- わられる数 = わる数 × 答え + 余り
例えば、10 / 4 = 2...2の確かめ算を行うと、
4 × 2 + 2 = 10
したがって、10 / 4 = 2...2は、正しい式といえます。
さいごに
今回はCASL2で除算する方法について見てきました。
CASL2で除算するプログラムを考えることで、除算の原理を再確認できた方もいると思います。
それでは次回にお会いしましょう。