アセンブリ言語 CASL2 で乗算する方法

乗算(かけ算)を加算(足し算)だけ行うにはどうやったらいいと思いますか?
実は、アセンブリ言語CASL2でかけ算を行う方法は3種類存在します。
でも、アセンブリ言語の加算命令だけでかけ算するプログラムを考えてみると意外と頭がこんがらがります。
今回は、CASL2による乗算の方法を共有したいと思います。
ループ処理による乗算
例1: 5 × 4 の計算
| 1 | MAIN | START | ||
| 2 | LD | GR1, A | ||
| 3 | LD | GR2, B | ||
| 4 | CALL | MUL | ;「MUL」サブルーチンの呼び出し | |
| 5 | ST | GR0, ANS | ;答え(積)をANS番地に格納 | |
| 6 | RET | |||
| 7 | ||||
| 8 | MUL | LAD | GR0, 0 | ;答え格納用にGR0を初期化 |
| 9 | LP | ADDA | GR0, GR1 | ;答えにかけられる数を加算 |
| 10 | LAD | GR2, -1, GR2 | ;かける数から1を減算 | |
| 11 | CPA | GR2, =0 | ;かける数と0を比較 | |
| 12 | JPL | LP | ;かける数が0より大きいならLPに移動 | |
| 13 | RET | |||
| 14 | ||||
| 15 | A | DC | 5 | ;かけられる数 |
| 16 | B | DC | 4 | ;かける数 |
| 17 | ANS | DS | 1 | ;答え |
| 18 | END |
※ シミュレータにそのままコピー&ペーストで使えます。
解説
ループ処理を用いた乗算は「かけられる数をかける数の分だけ足す」という乗算の基本的な仕組みを使っています。
例えば「5 × 4」は5を4回加算することで実現していますよね。
- 5 × 4・・・5 + 5 + 5 + 5
したがって、CASL2でも5を4回加算し乗算を実現します。
その際にループ処理を使って、かけられる数である5を加算する度にかける数の4から1を引き、4が0になった時点でループを抜ける、という処理によって4回のループを行います。
すなわちかける数の分だけループするということになります。
- かける数 = ループ回数
シフト演算による乗算
例2: 5 × 9 の計算
| 1 | MAIN | START | ||
| 2 | LD | GR1, A | ||
| 3 | LD | GR2, B | ||
| 4 | CALL | MUL | ;「MUL」サブルーチンの呼び出し | |
| 5 | ST | GR0, ANS | ;答えをANS番地に格納 | |
| 6 | RET | |||
| 7 | ||||
| 8 | MUL | LAD | GR0, 0 | ;答え格納用にGR0を初期化 |
| 9 | LP | LD | GR3, GR2 | ;編集用にかける数をGR3にコピー |
| 10 | AND | GR3, =#0001 | ;かける数の1ビット目が1か0か判定 | |
| 11 | CPA | GR3, =0 | ;かける数と0を比較 | |
| 12 | JZE | ZERO | ;かける数が0ならZEROに移動 | |
| 13 | ADDA | GR0, GR1 | ;答えにかけられる数を加算 | |
| 14 | ZERO | SLL | GR1, 1 | ;かけられる数を1ビット左シフト |
| 15 | SRL | GR2, 1 | ;かける数を1ビット右シフト | |
| 16 | CPA | GR2, =0 | ;かける数と0を比較 | |
| 17 | JNZ | LP | ;かける数が0でないならLPに移動 | |
| 18 | RET | |||
| 19 | ||||
| 20 | A | DC | 5 | ;かけられる数 |
| 21 | B | DC | 9 | ;かける数 |
| 22 | ANS | DS | 1 | ;答え |
| 23 | END |
※ シミュレータにそのままコピー&ペーストで使えます。
解説
シフト演算を用いた乗算は、2進数の乗算の筆算を基に組まれています。
このシフト演算を用いた乗算は、例1のループ処理を用いた乗算よりも行数が多いにも関わらず高速に動作するはずです。
計算対象の数が100や1000と大きくなるほど処理速度に差が出ます。
ちなみに、このプログラムの原理は乗算回路にも使用されています。
【5 × 9 の計算】
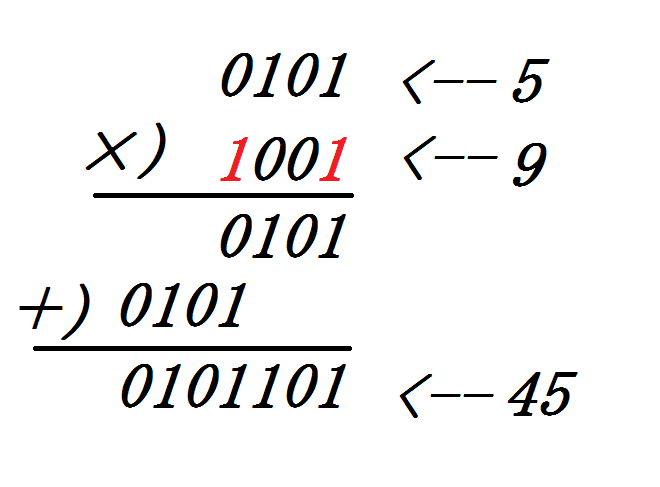
- まず、かけられる数(5)とかける数(9)を2進数にして考える。
- 筆算の式にする。
- 2進数のかける数の各桁を見て1になっている桁位置に、かけられる数を書き込む。
- 書き込んだかけられる数の総和が答え。
シフト演算は、かける数(2進数)の桁で1になっている位置に、かけられる数を移動(シフト)させるために使用します。
再起処理による乗算
例3: 5 × 2 の計算
| 1 | MAIN | START | ||
| 2 | LAD | GR0, 0 | ;答え格納用にGR0を初期化 | |
| 3 | LD | GR1, A | ||
| 4 | LD | GR2, B | ||
| 5 | CALL | MUL | ;「MUL」サブルーチンの呼び出し | |
| 6 | ST | GR0, ANS | ;ANS番地に答えを格納 | |
| 7 | RET | |||
| 8 | ||||
| 9 | MUL | CPA | GR2, =0 | ;かける数と0を比較 |
| 10 | JZE | FIN | ;かける数が0ならFINに移動 | |
| 11 | LAD | GR2, -1, GR2 | ;かける数から1を減算 | |
| 12 | CALL | MUL | ;再起処理 | |
| 13 | ADDA | GR0, GR1 | ||
| 14 | FIN | RET | ||
| 15 | ||||
| 16 | A | DC | 5 | ;かけられる数 |
| 17 | B | DC | 2 | ;かける数 |
| 18 | ANS | DS | 1 | ;答え |
| 19 | END |
※ シミュレータにそのままコピー&ペーストで使えます。
解説
再起処理を利用した乗算は、再起処理によって加算を繰り返すことで実現しています。
例1のループ処理を用いた乗算と原理が似ており、ループ処理が再起処理に置き換わっただけのものになります。
すなわち、かける数が再起する数ということになります。
- かける数 = 再起の回数
とはいっても、再起処理自体がすぐに理解しにくいものなので、意味が解るまで時間がかかるかもしれません。
どうしてもしんどいときは一旦止めてしまうのが吉です。
また、一息ついたらまた考え始めると不思議と理解できるようになるので無理なくゆっくり取り組んでみてください。
さいごに
今回はCASL2で乗算を実現する方法について見てきました。
CASL2でも乗算用の命令が用意されていれば、苦労することはないのですが、教育用ですから仕方ありませんよね。
それでは次回にお会いしましょう。