16進数のマイナスの数

16進数でマイナスの値を表すとき、符号がついていないので分かり難いですよね。
10進数であれば「-1」というように符号を使ってマイナスを表せますが、16進数や2進数などの10進数以外の記数法では符号を使いません。
今回は16進数でマイナスの数について情報を共有したいと思います。
16進数のマイナス数と同じ値になる数
16進数は、マイナスの数と大きな数が同じ表記になってしまいます。
実は、16進数で (FFFF)16 は10進数の65535であり、-1でもあります。
- (FFFF)16 = 65535
- (FFFF)16 = -1
なぜ、同じ値になるのか、まずは16進数を2進数に変換して考えると分かりやすいので変換してみます。
16進数を2進数に変換
16進数は、2進数を4桁ずつにまとめたものなので2進数に変換することで、数値の表す意味を確認することができます。
つまり、16進数とは長ったらしい2進数を見やすく4桁ずつにまとめて表現したものと認識しておいて問題ありません。
以下の図のように、16進数の各桁をそのまま2進数に当てはめて変換すればOKです。
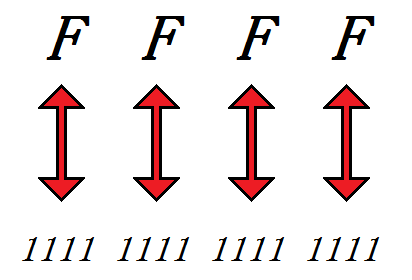
(F)16 は、2進数の (1111)2 になるので、桁の重みなどを特に気にせずに、各桁を分けてそのまま変換できます。
逆に、2進数から16進数への変換も全く同じです。2進数を4桁ずつ分けて、分けられたそれぞれの値を16進数で使われている数字に当てはめればOKです。
結果、(FFFF)16 を2進数に変換すると、(1111 1111 1111 1111)2 になりますね。
【16進 → 2進 変換】- (FFFF)16 = (1111 1111 1111 1111)2
これで、2進数への変換が終わりました。
次は、変換した数値の最上位ビットの扱い方の違いが関係しているので見てみます。
最上位ビットの扱いの違いでマイナス値を表せる
2進数は、最上位ビットの扱い方によってマイナス値として表すことができます。
(FFFF)16 を2進数に変換することで、(1111 1111 1111 1111)2 が導き出されましたが、この数の最上位ビットの扱い方を変えることで、65535と-1の両方を表すことができます。
ここで、最上位ビットとはビット列の最も左の桁を指します。
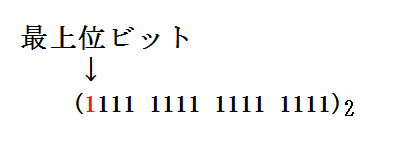
※ 最上位ビットはMSB(Most Significant Bit)とも呼ばれます。
(1111 1111 1111 1111)2 という数字は、最上位ビットを符号として扱うと、-1に、単なる桁の一部として扱うと65535になります。
また、最上位ビットを符号として扱うことを、「符号あり(Signed)」、符号としてではなく単なる桁の一部として扱うことを「符号なし(Unsigned)」と呼びます。
【最上位ビットの扱い方】- 符号として扱う・・・(1111 1111 1111 1111)2 = -1
- 単なる桁の一部として扱う・・・(1111 1111 1111 1111)2 = 65535
ちなみに、最上位ビットが1のときはマイナスの値を、最上位ビットが0のときはプラスの値を表しています。
| 最上位ビット | 符号の種類 |
| 1 | マイナスの値を表す |
| 0 | プラスの値を表す |
最上位ビットを符号として扱っているのか否かに関係なく、16進数では (1111 1111 1111 1111)2 を (FFFF)16 と表さないといけないため、16進数のままだと分かり難かったということがいえます。
以上のようにして、16進数では最上位ビットの扱いの違いで、マイナスの数と大きな数とを区別しています。
しかし、なぜオールビット1の2進数 (1111 1111 1111 1111)2 は、-1ということになるのでしょうか?。
それは2の補数表現が関係しています
2の補数によるマイナス表現
2進数でマイナス値を表す場合、2の補数を使用することができます。
2の補数は、計算対象の2進数を全ビットを反転させ +1することで求めることができます。
2進数では2の補数を求める = マイナスの数ということもいえます。
補数については「【計算なし】補数を求める方法」の記事へ。
以下に2の補数でのマイナスの数の求め方です。
例1: 2進数 -15 を求める

このようにして (1111)2 の全桁のビットを反転させた後に、+1することで、-15が求められました。
- (0001)2 = -15
念のためもうーつの例を見てみます。
例2: 2進数 -1 を求める
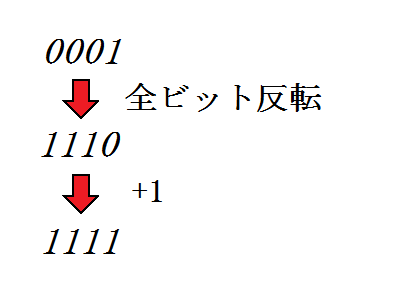
こちらの場合も、(0001)2 の全桁のビットを反転させた後に、+1することで、-1が求められました。
- (1111)2 = -1
ここで、あることに気付きませんか?
例1の-15を求める場合と例2の-1を求める場合が、真逆の結果になっているのです。
【15 と -15】- (1111)2 = 15
- (0001)2 = -15
【1 と -1】
- (0001)2 = 1
- (1111)2 = -1
つまり、2進数では 15 = -1、1 = -15 ということになります。
実は、(1111 1111 1111 1111)2 が、-1でもあり65535でもある理由です。
これらの関係が成立する上で、欠かせない要因があるのでそれについて見てみたいと思います。
マイナス値と最大桁数
実はこの「-1 = 65535」や「-1 = 15」などは、ある桁数の範囲内における最大値が -1 であるという法則があります。
例えば、前述した2進数の 15 = -1 や 1 = -15 が成立するには、最大桁数が4桁である必要があります。
4桁だと、(0000)2 ~ (1111)2 = 0 ~ 15 まで表せるので、4桁の最大値は15ということになります。
したがって、-1は、この15と同じ値になります。
また、-1 = 65535 が成立するには、最大桁数が16桁である必要があります。
16桁だと、(0000 0000 0000 0000)2 ~ (1111 1111 1111 1111)2 = 0 ~ 65535 まで表せるので、16桁の最大値は65535ということになります。
したがって、-1は、この65535と同じ値ということになります。
このように、マイナスの数がどのような値になるかは桁数の最大が何桁かで決まるということがいえます。
結論: 16進数のマイナスの数は2の補数を変換したもの
16進数のマイナスの数は、2の補数を4桁ずつに区切って変換した数です。
ここまでで、2進数(0001)2 の2の補数を求めると (1111)2 になり、これが10進数の-1ということでした。

その2進数4桁そのまま16進数に変換し、(1111)2 = (F)16 = -1 のようにすれば、16進数のマイナスの数ができあがるというわけです。
完全に3段論法...(笑)
2の補数表現と混同されがちなマイナス表現
ここからは少しややこしい話なので、いまいち16進数や2進数に慣れていないという方は、読まずに飛ばしてしまって大丈夫です。
前章内で、2の補数を用いてマイナス値を表す方法に触れました。
その際、最上位ビットの扱いの違いがマイナスかプラスかを分けるということを述べましたが、
2の補数による表現以外にも符号ビットによるマイナスの表現方法も存在するので紹介したいと思います。
符号ビットによるマイナスの表現
符号ビットによるマイナスの表現は、2の補数による表現と同様に最上位ビットによってマイナス値とプラス値を分ける方法です。
どのように値をプラスからマイナスに変換するのか16桁の例で見てみましょう。
例3: (0000 0000 0000 0001)2 の符号ビットによるマイナス表現
(0000 0000 0000 0001)2 = 1
↓↓↓ マイナスへ...
(1000 0000 0000 0001)2 = -1
単純に、最上位ビットを1に変えるだけです。
これで、-1ということになります。
この符号ビットによるマイナス表現は、2の補数のように数を反転してから +1 などの処理は必要ありません。
また、1のときはマイナスを、0のときはプラスの値を表します。
| 最上位ビット | 符号の種類 |
| 1 | マイナスの値を表す |
| 0 | プラスの値を表す |
これは、2の補数のときと同じですね。
しかし、この方法は、+0と-0が存在してしまうという最大の難点を持っています。
- (1000 0000 0000 0000)2 = -0
- (0000 0000 0000 0000)2 = +0
2の補数による表現との違い
2の補数による表現も符号ビットによる表現も、最上位ビットの扱い方が全く同じため混同されてしまう、ということがあります。
この符号ビットによる表現は、最上位ビットを0、1の違いでマイナス、プラスを表現する単なる決まりごとであるのに対して、
2の補数によるマイナス表現は、2の補数の算出することで、結果的に最上位ビットが1のときはマイナスで、0のときはプラスになってしまっているという違いがあります。
尚、最上位ビット以外は全く数字の配列が違うので、注意して下さい。
【2の補数による表現の例】- (1111 1111 1111 1111)2 = -1
- (1111 1111 1111 1110)2 = -2
- (1000 0011 0000 0000)2 = -32000
【符号ビットによる表現の例】
- (1000 0000 0000 0001)2 = -1
- (1000 0000 0000 0010)2 = -2
- (1111 1101 0000 0000)2 = -32000
こうして見ると符号ビットによる表現の方が直感的に分かりやすいですね。
さいごに
16進数や2進数のマイナスの表現はややこしいですね。
ともあれ「16進数のマイナスの数 = 2の補数を4桁に区切って16進数に変換した数」と考えておけば分かりやすいと思います。
それでは次回にお会いしましょう。